第3回 基礎解析

1. 微分可能性

   　関数 ｙ＝f(x) のグラフで x = a の点における接線を引くにはどうしたらいいか?
   
   　そもそも直線は通過点と傾きがわかると決まる。通過点は、まさに点(a, f(a)) だから、傾きmがどうにかして分かればいい。この傾きを与えるのが、微分という演算である。
   
   
   1. 定義
      
      極限計算の基本式(補足)参照.
      
      ＊　増分ｈは決して０にならない。０にならずに限りなく０に近づく。
      ＊　ｈの０への近づき方は、任意である。どんな近づき方をしても、同一の値に近づくとき極限が定まる（収束する）という（補足参照）。
      
      微分係数 f'(a) は点(a, f(a)) におけるこの関数のグラフの接線の傾きである。
      
      
      

   2. 微分係数の例
      1. ｙ＝f(x)＝３ｘ＋１のｘ＝２における微分係数を求める。
         
         
      2. ｙ＝f(x)＝ｘ²＋１のｘ＝２における微分係数を求める。
         
         

   3. 微分可能関数
      　定義
      　関数 f(x) が 定義域のすべての点で微分可能であるとき、f(x) を微分可能関数という。
      
      　微分可能関数とは、その関数のグラフが、なめらかにつながっている（すべての点で、切れてなく、孤立してなく、折れていない）ような関数である。
      
      　微分可能でない関数のグラフ
      　
   
   
   

2. 導関数

   1. 定義
      関数 y＝f(x) が微分可能関数であるとき、x=a に対してその微分係数を対応させる
      
      　　　a －－＞　f’(a)
      
      が定義される。この新しい関数を f(x) の導関数といい、
      
      　　　y = f’(x)
      
      とかく。
      
      

   2. 導関数の例
      1. ｙ＝f(x)＝３ｘ＋１　の導関数を求める。
         
         したがて、求める導関数は、ｆ’（ｘ）＝３　・・・（答)
         
         
      2. ｙ＝f(x)＝ｘ²＋１　の導関数を求める。
         
         したがって、求める導関数は、ｆ’（ｘ）＝２ｘ　・・・（答)
         
         今後、導関数を求めるときは、ｘ　のまま計算を行う。
         
         
      3. ｙ＝f(x)＝ｘⁿ　の導関数を求めよ。
         
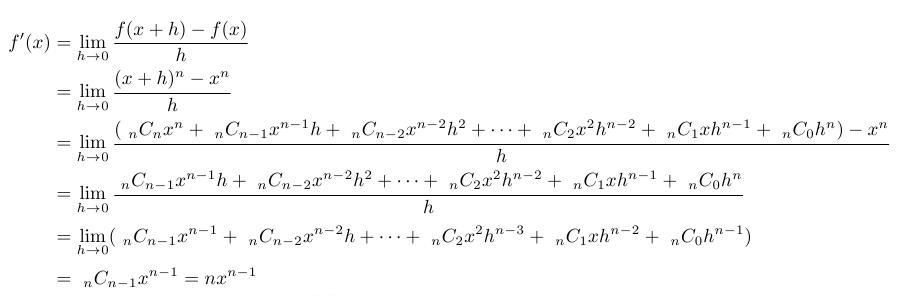
         したがって、求める導関数は、ｆ’（ｘ）＝nｘ^n-1　・・・（答)

3. 導関数（微分）の公式

   ｙ＝f(x)、ｙ＝g(x)　ともに微分可能関数とする。このとき、以下の５つの公式が成り立つ。
   1. 和
      
      証明
      
      
      
   2. 差
      
      証明
      
      
   3. 定数倍（ｋ：定数）
      
      証明
      
      
   4. 積
      
      証明
      
      
   5. 商（ｇ（ｘ）≠０）
      
      証明
      
      

   公式を用いた導関数の求め方
   
   ｙ＝f(x)＝３ｘ⁴＋２ｘ³－４ｘ²＋５ｘ－２
   
   の導関数は、上記公式の１，２，３を用いて、次のように計算してよい。
   
   f'(x)＝３（ｘ⁴）’＋２（ｘ³）’－４（ｘ²）’＋５（ｘ）－（２）’
   
   ＝３×４ｘ³＋２×３ｘ²－４×２ｘ＋５
   
   ゆえに、
   f'(x)＝１２ｘ³＋６ｘ²－８ｘ＋５　・・・（答）

1. 極限計算の基本式
   
   
   
2. 微分可能関数でない例
   
   
   
   
3. 数列の収束(極限値)について
   
   1. 定義 　無限数列 {a_n}：　a₁、a₂、・・・、a_n、・・・
      が α に収束するとは、
      
      　任意の正の数εに対して、ある番号 N が取れて
      N より大きなすべての番号 n で、｜a_n －α｜＜ε
      が成り立つこと、
      
      と定める。このとき、
      
      lim_n->∞a_n＝α
      
      と書く。
      解説　αの回りにどんな小さな幅εを指定しても、この小さな幅ε中に無限個の項が存在するとき、αに収束すると定める。幅εの中に入らないのは高々有限個に過ぎない。
      
      
   2. 収束しない場合
      　a_n＞２（n＝1,2,・・・）のとき、無限数列 {a_n} は 「1/2 に収束しない」と考える（これを「収束する」というには違和感があるでしょう！）。
      　これを上述のような言い方をまねると、
      ある幅ε（＝3/2）があって、どんな番号Nをとっても
      Nより大きなある番号ｎがあって、　｜a_n－1/2｜≧ε　が成り立っている。
      この否定（収束する場合）が、上述した述べ方である。
      
      
   3. 例
      　a_n＝1/n　のとき、lim_n->∞a_n＝0
      証明
      　任意の正の数εに対して、N＝[1/ε]＋１（[ x ] ： x を越えない最大の整数）とすると、
      Nよりおおきな整数nに対して、
      n＞N＞1/ε　より　1/n＜1/N＜ε
      よって、
      ｜a_n－0｜＝｜a_n｜＝｜1/n｜＝1/n＜ε
      ゆえに、数列{a_n}は、0に収束する（ lim_n->∞a_n＝0 ）。
      証明終
      
      
   4. 定理「有界な単調数列は収束する」
      　単調増加数列：　すべての番号 n で、a_n＜a_n+1
      　単調減少数列：　すべての番号 n で、a_n＞a_n+1
      
      
4. 関数の収束(極限値)について
   定義
   　ｘが限りなくaに近づくとき、関数f(x)がαに収束するとは、
   
   　任意の正の数εに対して、ある正の数δが存在して、
   　0＜｜ｘ－a｜＜δならば｜f(x)－α｜＜ε
   　が成り立つときをいう。
   　これを、
   
   　lim_x->af(x)＝α
   
   　と書く。
   　（注:不等式　0＜｜ｘ－a｜は決して＝にはならない。）

1. 関数　ｙ＝f(x)＝x³－4x²－3x－１　について
   
   
   1. 関数f(x)の導関数を求めよ。
      
      
   2. ｘ＝２における、この関数のグラフの接線の方程式を求めよ。
      
      
   3. 上問２で求めた接線とグラフの他の交点を求めよ。
      
      
   
   
2. 導関数（微分）の公式を使って、次の関数を微分せよ。
   1. 
      
      
   2. 
      
   
   
3. 次の各問に答えよ。
   
   
   

2022年（令和4年）6月17日更新